ParametricPlot[{5 Cos[(-11 t/5)] + 7 Cos[t], 5 Sin[(-11 t/5)] + 7 Sin[t]}, {t, 0, 10 Pi}, AspectRatio -> Automatic]

Integrate[Sqrt[D[{5 Cos[(-11 t/5)] + 7 Cos[t], 5 Sin[-11 t/5] + 7 Sin[t]}, t] . D[{5 Cos[(-11 t/5)] + 7 Cos[t], 5 Sin[(-11 t/5)] + 7 Sin[t]}, t]], {t, 0, 10 Pi}]

�� _ 0^(10 ��) �� ((7 Cos[t] - 11 Cos[(11 t)/5])^2 + (-7 Sin[t] -11 Sin[(11 t)/5])^2) d t

 

curvature[c_][t_] := Det[{D[c[tt], tt], D[c[tt], {tt, 2}]}]/((D[c[tt],tt] . D[c[tt], tt])^(3/2)) /. tt -> t

radiuscurvature[c_][t_] := Abs[1/curvature[c][tt]] /. tt-> t

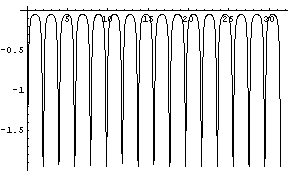
c[t_] = {5 Cos[(-11 t/5)] + 7 Cos[t], 5 Sin[(-11 t/5)] + 7 Sin[t]} ; Plot[curvature[c][t], {t, 0, 10 Pi}]

Converted by Mathematica  (February 26, 2004)